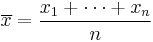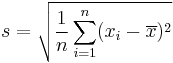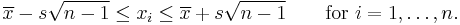Samuelson's inequality

In statistics, Samuelson's inequality, named after the economist Paul Samuelson,[1] also called the Laguerre–Samuelson inequality,[2] after the mathematician Edmond Laguerre, states that every one of any collection x1, ..., xn, is within √(n − 1) standard deviations of their mean. In other words, if we let

\overline{x} = \frac{x_1%2B\cdots%2Bx_n}{n}

be the mean and

s = \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2 }

be the standard deviation, then

\overline{x} - s\sqrt{n-1} \le x_i \le \overline{x} %2B s\sqrt{n-1}\qquad \text{for }i = 1,\dots,n. [3]

Equality holds on the left if and only if the n − 1 smallest of the n numbers are equal to each other, and on the right iff the n − 1 largest ones are equal.

Samuelson's inequality may be considered a reason why studentization of residuals should be done externally.

References

  1. ^ Paul Samuelson, "How Deviant Can You Be?", Journal of the American Statistical Association, volume 63, number 324 (December, 1968), pp. 1522–1525 JSTOR 2285901
  2. ^ Jensen, Shane Tyler (1999) The Laguerre–Samuelson Inequality with Extensions and Applications in Statistics and Matrix Theory MSc Thesis. Department of Mathematics and Statistics, McGill University.
  3. ^ Advances in Inequalities from Probability Theory and Statistics, by Neil S. Barnett and Sever Silvestru Dragomir, Nova Publishers, 2008, page 164